Introduction
在写复变论文的过程中,因为我写的主要是关于留数定理的内容,避免不了要用围道积分。一开始我只是想口头叙述围道长什么样就好了,但是复变函数II的期末考试就是一篇论文,想想还是更加慎重一点,所以就自学了latex绘图.
Latex绘图主要是用tikz包
在开头需使用
1
\usepage{tikz}
Example 1
在计算欧拉积分时,我们需要考虑如下围道
\[\bar{\Gamma}=\Gamma_1\cup\Gamma_2\cup\Gamma_3\cup\Gamma_4\] \[\left\{ \begin{aligned} &\Gamma_1:\left\{z|r\leq z\leq R\right\}\\ &\Gamma_2:\left\{z|z=Re^{i\theta},0\leq\theta\leq\alpha\right\}\\ &\Gamma_3:\left\{z|z=le^{i\alpha},R\geq\theta\geq r\right\}\\ &\Gamma_4:\left\{z|z=re^{i\theta},\alpha\geq\theta\geq0\right\} \end{aligned} \right.\]围道示意图如下:
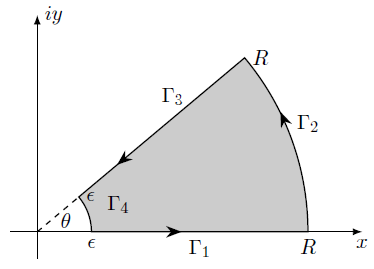
具体的 Latex 代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
\begin{center}
\begin{tikzpicture}[>={Stealth[length=0.3cm]},
decoration={markings,
mark= at position .1 with {\arrow{<}},
mark= at position .45 with {\arrow{<}},
mark= at position .83 with {\arrow{<}},
}
]
\def\angle{40}
\def\bigradius{5}
\def\littleradius{1}
\filldraw[postaction = {decorate}, thick ,fill=gray!40]
(\angle:\littleradius) node[right]{$\epsilon$}
-- (\angle:\bigradius) node[right]{$R$}
arc(\angle:0:\bigradius) node[below]{$R$}
-- (\littleradius,0) node[below]{$\epsilon$}
arc (0:\angle:\littleradius) -- cycle;
\draw[dashed,thick] (0,0) node[xshift=15pt, yshift=6pt]{$\theta$} -- (\angle:\littleradius);
\node at(3,-0.3){$\Gamma_1$};
\node at(5,2){$\Gamma_2$};
\node at(2.5,2.5){$\Gamma_3$};
\node at(1.5,0.5){$\Gamma_4$};
\draw[-Latex] (-0.1*\bigradius,0) -- (1.2*\bigradius,0) node[below]{$x$} ;
\draw[-Latex] (0,-0.1*\bigradius) -- (0,4) node[right]{$iy$};
\end{tikzpicture}
\end{center}
Example 2
在计算高斯积分时,我们可以考虑一种不同于课本方式的围道计算,如下图所示:
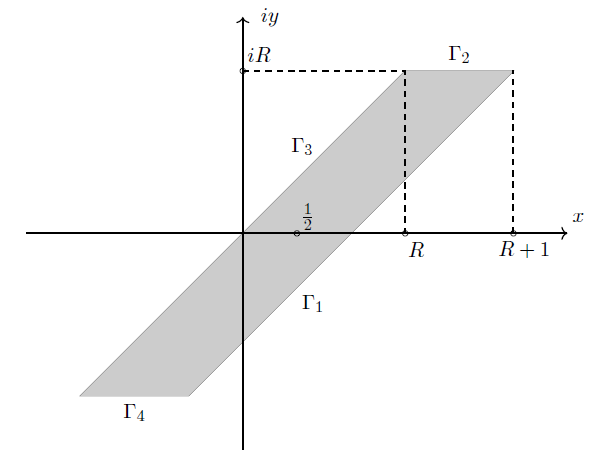
具体的 Latex 代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
\begin{center}
\begin{tikzpicture}
\def\gap{0.2}
\def\bigradius{3}
\def\littleradius{0.5}
% Axes
\draw[->](-1,-3) -- (5,3) -- (3,3) -- (-3,-3) -- (-1,-3) --cycle;
\fill[gray!40](-1,-3) -- (5,3) -- (3,3) -- (-3,-3) -- (-1,-3) --cycle;
\draw [thick,->] (-4, 0) -- (6,0);
\draw [thick,->] (0, -4) -- (0,4);
\node at (0.5,4){$iy$};
\node at (6.2,0.3){$x$};
\node at (1.3,-1.3){$\Gamma_1$};
\node at (4,3.3){$\Gamma_2$};
\node at (1.1,1.6){$\Gamma_3$};
\node at (-2,-3.3){$\Gamma_4$};
\draw(1,0) node[shape=circle,draw,inner sep=1pt]{};
\node at (1.2,0.3){$\frac{1}{2}$};
\draw(3,0) node[shape=circle,draw,inner sep=1pt]{};
\node at (3.2,-0.3){$R$};
\draw(5,0) node[shape=circle,draw,inner sep=1pt]{};
\node at (5.2,-0.3){$R+1$};
\draw(0,3) node[shape=circle,draw,inner sep=1pt]{};
\node at (0.3,3.3){$iR$};
\draw[dashed, thick] (0,3)--(3,3)--(3,0);
\draw[dashed, thick] (5,0)--(5,3);
%\draw[fill=gray,domain=-3:3]plot({\x-2},\x);
\end{tikzpicture}
\end{center}
Example 3
在计算高斯积分时,我们发现可以对高斯积分进行推广,进而得到 $e^{-a\sqrt{\pi}}$ 的拉普拉斯逆变换,在计算中,我们需要考虑如下图所示的积分围道:
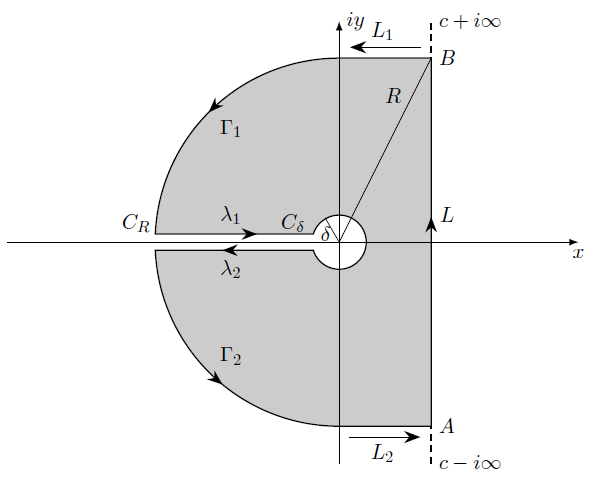
具体的 Latex 代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
\begin{center}
\begin{tikzpicture}[>={Stealth[length=0.3cm]},
decoration={markings,
mark= at position .15 with {\arrow{>}},
mark= at position .3 with {\arrow{>}},
%mark= at position .42 with {\arrow{>}},
mark= at position .49 with {\arrow{>}},
mark= at position .63 with {\arrow{>}},
mark= at position 0.9 with {\arrow{>}},
}]
\def\radius{3.4}
\def\bigradius{3.4}
\def\littleradius{0.5}
\def\angle{60}
\def\gap{0.3}
\draw[dashed,thick]
let
\n0 = {cos(\angle)},
in
(\radius*\n0,-\radius*1.2) node[right]{$c - i\infty$}-- (\radius*\n0,\radius*1.2)node[right]{$c+i\infty$};
% contour
\filldraw[postaction = {decorate}, thick ,fill=gray!40]
let
\n1 = {asin(\gap/2/\bigradius)},
\n2 = {asin(\gap/2/\littleradius)}
in
(0.5*\bigradius,\bigradius)node[right]{$B$}--(0,\bigradius) arc(90:180-\n1:\bigradius) --(-\n2:-\littleradius) arc (-\n2:-(360-\n2):-\littleradius) --(\n1:-\bigradius) arc(180+\n1:270:\bigradius)--(0.5*\bigradius,-\bigradius)node[right]{$A$}--(0.5*\bigradius,\bigradius);
\draw (0,0) -- (0.5*\bigradius,\bigradius) node[xshift=-20pt,yshift=-20pt]{$R$};
\draw (0,0) -- (2*\angle:\littleradius) node[xshift=0pt,yshift=-8pt]{$\delta$};
\node[xshift=-10pt,yshift=10pt] at (-\bigradius,0){$C_R$};
\node[xshift=-10pt,yshift=10pt] at (-\littleradius,0){$C_{\delta}$};
\draw[->](1.5,3.6)--(0.2,3.6);
\node at (0.8,3.9){$L_1$};
\draw[->](0.2,-3.6)--(1.5,-3.6);
\node at (0.8,-3.9){$L_2$};
\node at(-2,2.1){$\Gamma_1$};
\node at(-2,-2.1){$\Gamma_2$};
\node at(-2,0.5){$\lambda_1$};
\node at(-2,-0.5){$\lambda_2$};
\node at(2,0.5){$L$};
% pole
%\fill (0,0) circle (3pt) ;
%\draw[-Latex] (0.6,-0.8) node[right]{pole} --(0.15,-0.15);
% axis
\draw[-Latex] (-1.8*\radius,0) -- (1.3*\radius,0) node[below]{$x$} ;
\draw[-Latex] (0,-1.2*\radius) -- (0,1.2*\radius) node[right]{$iy$};
\end{tikzpicture}
\end{center}
Example 3
在计算狄利克雷积分时,我们需要考虑一种围道计算,如下图所示:
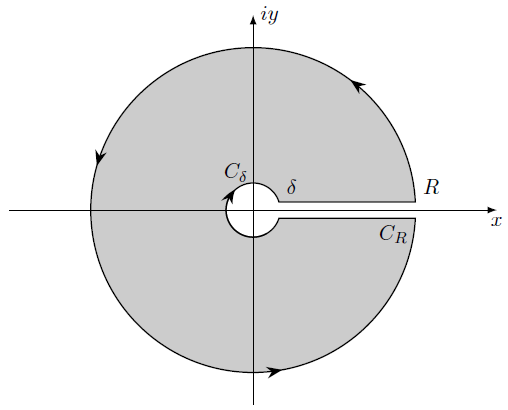
具体的 Latex 代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
\begin{center}
\begin{tikzpicture}[>={Stealth[length=0.3cm,bend]},
decoration={markings,
mark= at position .1 with {\arrow{>}},
mark= at position .32 with {\arrow{>}},
mark= at position .55 with {\arrow{>}},
% mark= at position 0.86 with {\arrow{>}},
}
]
\def\gap{0.3}
\def\bigradius{3}
\def\littleradius{0.5}
\filldraw[postaction = {decorate}, thick ,fill=gray!40]
let
\n1 = {asin(\gap/2/\bigradius)},
\n2 = {asin(\gap/2/\littleradius)}
in
(0+\n1:\bigradius) node[above right]{$R$} arc (0+\n1:360-\n1:\bigradius) node[below left]{$C_{R}$} -- (0-\n2:\littleradius) arc (360-\n2:0+\n2:\littleradius) node[above right]{$\delta$} -- cycle;
\draw[thick,->] (300:\littleradius) arc (300:130:\littleradius) node[above]{$C_{\delta}$};
%\fill (-1.2,0) circle (3pt) ;
%\draw[->] (-1.2,-1) node[right]{pole} --(-1.2,-0.15); % <--
\draw[-Latex] (-1.5*\bigradius,0) -- (1.5*\bigradius,0) node[below]{$x$} ;
\draw[-Latex] (0,-1.2*\bigradius) -- (0,1.2*\bigradius) node[right]{$iy$};
\end{tikzpicture}
\end{center}
Remark
If you have any questions or need further assistance, feel free to ask! Here is my email: nkusherr1 at gmail.com